SemiNMF-PCA framework for Sparse Data Co-clustering

Allab, Labiod, and Nadif (2016) in CIKM
Research Paper

Presented by
Christian Bager Bach Houmann @ AAU

9 Jan 2024

The problem

• Given a large set of documents and their content, how can we group them into topics and understand which terms are typically associated?
• Existing methods struggle with high-dimensionality and sparsity in document-term matrices, doesn’t capture the underlying geometry well
• Most clustering approaches only focus on documents or terms, but not both (unilateral clustering)
• Using PCA and then k-means clustering (Tandem clustering) is discouraged

Proposed solution: Integrating SemiNMF and PCA

Discouraged because it may not reveal the true cluster structure because the first few principal components of PCA may not reflect it.

Understanding the SemiNMF-PCA Framework for Sparse Data Co-clustering

• Semi non-negative matrix factorization (SemiNMF)
• Principal Component Analysis (PCA) for
• Sparse data
• Co-clustering

Sparse, High-Dimensional Data

• Sparse Data: Dataset where most entries are zero
• High Dimensionality: Datasets with a large number of features (e.g., terms in text dataset)
• Key Challenges:
  • Difficulty in visualizing and understanding the structure
  • Traditional clustering methods fall short in capturing the underlying patterns

Brief introduction to NMF and PCA

• Nonnegative Matrix Factorization (NMF):
  • Decomposes data matrices into parts for easier interpretation
  • Data must be non-negative
• Principal Component Analysis (PCA):
  • Reduces dimensions while keeping the most important variability

Co-clustering

• What is Co-clustering?
  • Simultaneous grouping of data points (e.g., documents) and features (e.g., terms).
• Why Co-clustering?
  • Often more effective than unilateral clustering, especially for sparse, high-dimensional data
• With matrix factorization
  • NMF for unilateral, then NMTF for co-clustering

NMTF creates a 3-factor decomposition - creates an approximation of the data matrix through:

• a row-coefficient matrix,
• a block value matrix,
• and a column-coefficient matrix – all are nonnegative.

The approximation is the product of these.

Co-clustering

Clustering vs. Co-clustering: Allab, Labiod, and Nadif (2016)

Matrix factorization based co-clustering algorithms

• Croeuc Algorithm: Uses the principle of double k-means to perform co-clustering on continuous data
• Bipartite Spectral Graph Partitioning Algorithm (Spec): Designed to be sequel to Croeuc
• Information-Theoretic Co-clustering (ITCC)
• Spectral Co-clustering Algorithm (SpecCo): Appears to perform well on document clustering

Locality Preserving based Co-clustering

• Drawback of other methods: they often overlook local manifold geometry because they mainly rely on global Euclidean geometry
• Dual Regularized Co-Clustering (DRCC): Combines NMTF with incorporating manifold structures in both sample and feature spaces. Limited in handling data with negative values and has high computational complexity.
• Locally Preserved Fast Nonnegative Matrix Tri-Factorization (LpFNMTF): Tries to reduce computational demands by enforcing constraints for factors to be cluster indicator matrices

Generally, a \(d\)-dimensional manifold is a part of an \(n\)-dimensional space (where \(d<n\)) that locally resembles a \(d\)-dimensional hyperplane.

Basically, “locally resembles” means that near each point, it looks like it resembles such a plane. So while the whole thing may look 3D, near each point, it looks 2D.

Local Geometrical Structure: This refers to the shape and connectivity of data points in a small, localized region of the dataset. It’s about understanding how data points are arranged or connected to each other in a close neighborhood.

SemiNMF

• Semi-nonnegative:
  • data \(X\) and cluster centroids \(S\) can be positive and negative, but
  • cluster indicator matrix \(G\) must be zero or positive: a data point has a non-negative degree of association with a cluster
• Soft clustering: a point can have partial membership to a cluster
• Goal is to minimize difference between \(X\) and \(GS^{\top}\)

Cluster centroid means a representative point that characterizes the central position / typical attribute of a cluster.

Cluster indicator indicates soft (not binary) membership with clusters for the various points. Higher values means a point is more strongly associated with a given cluster.

PCA

• Used to find lower-dimensional subspace best representing the data
• Done by identifying principal directions \(Q\) and projecting the data points into this new subspace, giving principal components \(U\)
• Goal is reconstructing \(UQ^{\top}\) as closely to \(X\) as possible, subject to \(Q^{\top}Q=I\) (ensures orthogonality)
• \(U\) can be considered continuous analogue to the discrete membership indicators in k-means
  • This is the basis for Laplacian embedding integration

Being = I means dot product of any pair in Q is 0: they’re orthogonal.

It’s important that the principal directions are orthogonal, as they need to capture unique variance, without redundancy.

\(U\) being continuous analogue to discrete membership indicators in k-means basically just refers to the membership indicators in k-means being binary (in or not in cluster), whereas being continuous would make it partial membership.

SemiNMF-PCA-CoClust

Form matrix \(M\) of size \((n+d)\times(n+d)\) from data \(X\): \[ M=\left[\begin{matrix} 0 & X \\ X^{\top} & 0 \end{matrix}\right] \]

• Obtain \(G\) by doing k-means clustering on \(X\) and \(X^{\top}\) - represents cluster membership for both samples and features
• \(S\) consists of centroid matrices for samples and features
• \(Q\) contains components reduced from SVD of \(X\)

Goal is minimizing: \[ \min_{G,S,Q}\| M-GSQ^{\top} \|^{2}\quad s.t.\quad G\geq 0, Q^{\top}Q=I \]

The optimization is about minimizing the Frobenius Norm of the difference between \(M\) and the product \(GSQ^{\top}\), subject to \(G\) being non-negative and \(Q^{\top}Q=I\) to ensure orthogonality in \(Q\).

Frobenius norm measures sum of squared differences between data and reconstruction.

G: Since we work on document-term matrices, it would mean that k-means on \(X\) is document clustering (document clusters is \(G_{g}\)) and on \(X^{\top}\) is term clustering (term clusters is \(G_{f}\)).

\(G\) is of size \((nd\times k\ell)\), S of size \((k\ell \times_{2}p)\), and \(Q\) of size \(nd\times_{2}p\), defined as: \[ G=\left[\begin{matrix} G^{(n\times k)}_{g} & 0 \\ 0 & G^{(d\times \ell)}_{f} \end{matrix}\right] \] where \(G_{g}\) and \(G_{f}\) are the label matrices obtained by using k-means on \(X\) and \(X^{\top}\), respectively.

S: \[ S=\left[\begin{matrix} S_{g}^{(k\times p)} & \theta_{g}^{(k\times p)} \\ \theta^{(\ell \times p)}_{f} & S^{\ell \times p}_{f} \end{matrix}\right] \] where \(S_{g}=(s_{k'p})\) and \(S_{f}=(s_{\ell'p})\) are centroid matrices, while \(s_{gk'}\) is a centroid of the \((k')^{th}\) sample cluster for each \(k'=1,\dots,k\) and \(s_{f\ell'}\) is a centroid of the \((\ell')^{th}\) feature cluster for each \(\ell'=1,\dots,\ell\). \(\theta_{g}\) and \(\theta_{f}\) contain non null values and involve mixed information of both samples and features.

Q: \[ Q=\left[\begin{matrix} Q^{(n\times p)}_{g} & 0 \\ 0 & Q^{(d\times o)}_{f} \end{matrix}\right] \] - Doing SVD on \(X\) gives \(U, \Sigma, V\). - We truncate those to the first \(p\) components to get an optimal rank-p approximation of \(X\) (this is a common approach in PCA for dimension reduction – PCA is just a specific application of SVD) - We form \(Q\) from \(Q_{g}=U\Sigma\) and \(Q_{f}=V\Sigma\), which captures the principal components for documents & terms respectively.

Regularized SemiNMF-PCA CoClust

• Uses graph Laplacian embeddings to account for intrinsic geometric structure
• Create KNN data graph for samples and features: data points connected to k nearest neighbors
  • Used to represent local proximity/similarity between points, capturing local structure and relationship in data
• Create weight matrices \(W_g\) and \(W_f\) from graph: represents connections in data samples and features, respectively
• Compute normalized graph Laplacians \(L_g\) and \(L_f\) from \(W_g, W_f\) and diagonal matrices of them

Graph Laplacian embeds especially supports data lying on non-linear manifolds. They’re used to preserve local relationships and maximize smoothness w.r.t data’s intrinsic manifold

The graph Laplacian is basically constructed in a way much similar to normal. Normally it’s \(L = D - A\) where \(D\) is a diagonal degree matrix and \(A\) is the adjacency matrix. In this case, we construct it from the weight matrices (similar to adjacency matrix, but with kn-neighbors) and \(D\) is obviously basically the same - but here it’s the row sums of the individual weight matrices.

Regularized SemiNMF-PCA CoClust

Introduce the normalized graph Laplacians in \(M\): \[ M=\left[\begin{matrix} \alpha L_{g} & X \\ X^{\top} & \beta L_{f} \end{matrix}\right] \] where \(\alpha\) and \(\beta\) are the regularization parameters used to control the contribution of \(L_{g}\) and \(L_{f}\) respectively.

The minimization problem is of the same form as before, but with updated \(M\).

\[ \min_{G,S,Q}\| M-GSQ^{\top} \|^{2}\quad s.t.\quad G\geq 0, Q^{\top}Q=I \]

Optimize by updating \(S\), \(G\), and then \(Q\) repeatedly until convergence.

At this point, they also show how they can decompose the optimization problem shown here into two terms.

\[ \|M-GSQ^{\top}\|^{2}=\|M-MQQ^{\top}\|^{2}+\|MQ-GS\|^{2} \]

The first term is the objective function of PCA (alternate form than the one I show), and the second is the SemiNMF criterion in a low-dimensional subspace.

Algorithm: Inputs: Data matrix \(X\), number of sample and feature classes \(k\) and \(l\), number of components \(p\).

We start by initializing \(G\) using spherical [[k-means]] and then \(Q\) using SVD.

Then we compute \(L_{g}\) and \(L_{f}\). Construct the matrix \(M\). And we start the approximation process, which is repeating the following until convergence: - Update \(S\) by \(S=(G^{\top}G)^{-1}G^{\top}MQ\) - Update \(G\) by \(G=G\circ \sqrt{ \frac{[MH^{\top}]^{+}+G[HH^{\top}]^{-}}{G[HH^{\top}]^{+}+[MH^{\top}]^{-}} }\) where \(H=SQ^{\top}\), \(A^{+}\) and \(A^{-}\) correspond respectively to positive and negative parts of the matrix \(A\) given by \(A^{+}_{ik}=\frac{1}{2}(|A_{ik}|+A_{ik})\) and \(A^{-}_{ik}=\frac{1}{2}(|A_{ik}-A_{ik})\). - Update \(Q\) by solving \(\min_{Q^{\top}Q=I}\|M-BQ^{\top}\|^{2}\) where \(B=GS\).

And then output: Sample indicator matrix \(G_{g}=G[1..n,1..k]\), feature indicator matrix \(G_{f}=G[n+1..nd, k+1..k\ell]\), and sample embedding matrix \(Q_{g}=Q[1..n, 1..p]\).

Experimental Results and Analysis

Performance Metrics

• Accuracy (Acc): correctness of cluster asignments
• Normalized Mutual Information (NMI): evaluate mutual information between cluster assignments and true labels
• Adjusted Rand Index (ARI): Assess similarity between clusterings and ground truth, adjusting for chance

Data and Parameters

• Datasets size and sparsity varied across datasets:
  • Samples (documents): min=~500, max=~20k
  • Features (terms): min=~1k, max=~43k
• Run each method w. different parameter settings 50x
• Reports best results per metod
• Grid search regularization parameter \(\alpha\) with \(\beta=\alpha0.1\) in grid \((0.01, 0.1, 1, 10, 100, 500, 1000)\)

Results

Allab, Labiod, and Nadif (2016)

The empirical evidence suggests that R-SemiNMF-PCA-CoClust often outperforms the compared algorithms.

Results: Statistical Tests

• One-way ANOVA & pairwise t-tests
• Show statistically significant performance increase over LpFNMTF

Allab, Labiod, and Nadif (2016)

• They only report the best runs. This doesn’t account for the variability and stability of the clustering results across runs. What if they took the average? Or remove outlier runs (or top & bottom 2) and took the average then? Could be useful to see the distribution of performances over multiple runs.
• The variability shown in the standard deviations in table 3 could indicate that could indicate that while R-SemiNMF-PCA-CoClust generally performs better, there is variability that could affect its reliability in certain cases. It’s still better than the other algorithm, also visible due to having less variability.
• But since they report variability, we get (some of) the added context that we desired here.

One-way ANOVA (Analysis of Variance) is used to determine if there are any statistically significant differences between the means of three or more independent (unrelated) groups. It compares the variance within groups to the variance between groups to ascertain if any of the group means are significantly different from each other.

Pairwise t-tests: used to compare the means of two groups at a time, to identify if they are significantly different from each other. It is often used after an ANOVA test when there are multiple groups, to find out which specific pairs of groups have significant differences in their means.

Cluster Visualization

Allab, Labiod, and Nadif (2016)

• The method groups clusters to provide clearer separation between them; there’s less overlap

Regularization parameters

Allab, Labiod, and Nadif (2016)

• CSTR: Performance increases with increase in \(\alpha\)
• Classic3: Optimal at \(\alpha=10\)
• Reviews: Performance decreases with increase in \(\alpha\)
• Choosing optimal parameters for datasets vs. generalization

• CSTR: Regularization enforcing certain geometric structures well-aligned with this dataset?
• Classic3: Too much regularization distorts natural clusters / fail to capture relationships?
• Reviews:
  • Could intrinsic structure in dataset be less aligned with the assumptions made by the regularization?
  • Authors say due to higher noise in data - or the data’s manifold is not well-captured by the chosen form of regularization

This figure makes it evident that they’ve chosen the optimal parameters for each dataset. That calls into question the generalizability of the method. If you have to vary your parameter values so much — having to tune them for each dataset — the algorithm may not perform well in practice, where we don’t have true labels to guide the tuning.

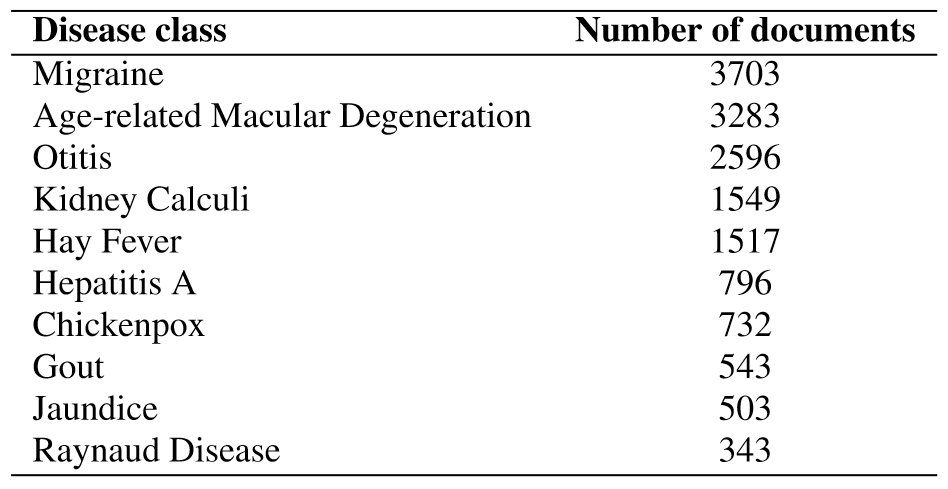
PUBMED

To illustate co-clustering capabilities on term clusters

The reason this is separate is because there’s no gold standard labels for terms, but they still wanted to assess term clustering (not just document-clustering, as shown earlier).

PUBMED10

• Biomedical abstracts categorized by disease
• Divided into
  • PUBMED10
  • PUBMED6
  • PUBMED5

Allab, Labiod, and Nadif (2016)

The PUBMED data set contains biomedical abstracts categorized by disease, which provides a natural grouping for documents and terms.

Results

Allab, Labiod, and Nadif (2016)

Dense bands of variables - terms cited in many docs - considered noise.

Results

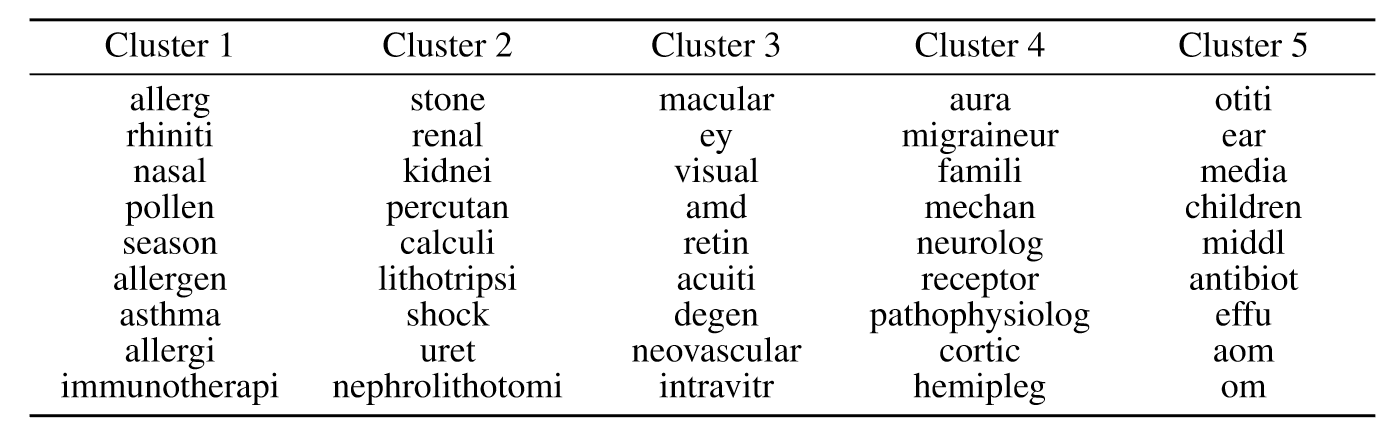
Allab, Labiod, and Nadif (2016)

• Identified semantically coherent column clusters indicative of document clusters - seems to correspond to diseases
• Found common terms between different diseases - showing ability to handle overlap and shared features between clusters

Dense bands of variables (terms cited in many documents) were considered as noise but did not affect the co-clustering process or the classification of documents and terms.

Conclusion

• Presented framework unifying dimensionality reduction and co-clustering
• Achieves better performance than previous methods

Critical Evaluation

Critical Evaluation: Limitations

• Motivation is lacking
• Questionable choices for mathematical terms
• Clear weakness that they didn’t evaluate co-clustering better; but they excuse it with there being no gold standard labels for terms.
• Unclear whether the method needs parameter tuning specific to the dataset¹, but it somewhat seems that way

1. Due to the results in Figure 3.

Critical Evaluation: Strengths

• Figures and illustrations were useful
• The frameworks seems to manage noise well¹
• Integration is well reasoned and grounded in theory
• Achieved statistically significant increase in performance over state of the art

1. Evident by PUBMED case results

Critical Evaluation: Additional points

• Would have liked to see performance over all runs, not just via variance (std dev).
• Computational complexity is not described; how does it compare to other SoTA algorithms?

Q&A

• Thank you for your attention!
• I am now ready to answer your questions and discuss further.

Allab, Kais, Lazhar Labiod, and Mohamed Nadif. 2016. “SemiNMF-PCA Framework for Sparse Data Co-clustering.” In Proceedings of the 25th ACM International on Conference on Information and Knowledge Management, 347–56. CIKM ’16. New York, NY, USA: Association for Computing Machinery. https://doi.org/10.1145/2983323.2983707.